

I never really understood General Relativity until I learned to sew, just as I never really understood thermodynamics until I learned to cook. As with cooking, I was driven to sewing by necessity: my jeans didn’t fit. The first modifications were small ones: darts here and there to pull in material, later I added elastic waistbands, then suspenders.
Eventually I got so fed up with the bad fit that I decided to make my own jeans from scratch. I bought a few yards of fabric, wrapped it around myself, and started cutting. Mistakes weren’t a problem: I knew how to patch and I figured I would just keep cutting and patching until the thing fit around my body. It took about a week for the carpet to slowly evolve into pantaloons. I finished them just in time to wear them when my wife came home from a conference, whereupon she exclaimed, “They’re purple!” Pants 1.0 have been described as part-Joker, part-Catwoman, and they lasted about a year.
Spending all that time with fabric forced me to think a lot about topology and curvature. I had to somehow reproduce my own curvature in cloth: too much curvature and it would bulge, too little and it would be tight. The most difficult part is the crotch, which bends upward in the front and back, but downward toward the legs. “Oh,” I realized, “That’s what it means to be negatively curved!” Zero and positive curvature are easy to understand from textbooks, but negative curvature is always drawn as a twisted bit of graph paper, mysteriously called a saddle-point. “Of course it’s a saddle,” I said to myself. “What else are saddles meant to fit?”
In popular explanations of General Relativity, it is common to say that space-time is like a rubber sheet, curving under the weight of planets and stars. The planets are marbles that someone has set on the rubber sheet, to show that the sheet does, in fact, bend. This explanation has always bothered me because the marbles are outside of the sheet. If the sheet is supposed to represent space, then everything ought to be within the sheet itself. Moreover, the demonstration only works because the real Earth is under the rubber sheet, drawing marbles toward itself.
And while sheets can be curved, what could it possibly mean for space to be curved? How could I ever visualize that?
In school, I learned about the mathematics of curvature and its application to space-time, the theory of gravitation known as General Relativity. The formal definition of curvature is based on an intuitive concept, but is complicated by the subtlety of continuity. Fabrics approximate continuity with small but not infinitesimal stitches, so in the end it was the ancient art of shaping cloth with thread that helped me to visualize curved space-time. Video games helped, too.
How is cloth like space? For this metaphor to work, we have to imagine being a drawing on the cloth— in other words, two-dimensional. I’ve only ever been two-dimensional in video games, such as the kind where I’m a dungeon with many rooms. Each room has a north, south, east, and west, but up and down are meaningless. There are doors at the edges of the room; these lead to other rooms, some with hidden treasure or monsters.
It looked a bit like this:

Video game character in a dungeon room with four exits: north, south, east, and west.
Video games aren’t usually projected in cloth, but there’s no conceptual reason not to— only technological. (Cloth computer screens would be pretty cool!) The way the character moves wouldn’t be altered by folding the cloth: adjacent stitches (pixels) are still adjacent when the cloth is folded. Our hero would crawl around the crease without ever realizing that his world isn’t spread flat.
His world can be changed, however, by how we sew it. Suppose that we sew the east door of the room to the west door: when our hero walks out through one door, he finds himself walking in through the other. His whole dungeon appears to be a long east-west corridor of identical rooms.

A dungeon room with the east door sewn to the west door, so that the character can go around and around.
These kinds of connections can be arbitrarily made in video games: the programmer just needs to type, “if (exit through west) then {enter through east;}.” It’s like a hyperlink on a web page. We could imagine something similar in our three-dimensional world without having to visualize it as a four-dimensional suture. While there isn’t any known way to make wormholes or looped spaces in reality, the idea is all over science fiction, from Madeleine L’Engle’s A Wrinkle in Time to Neil Gaiman’s Coraline.
In this article, I’d like to talk about a different kind of connection. A looped space is made from one weird connection— curvature is made from weird connections all over the place.
Suppose that we build a dungeon from a network of linked rooms with two north doors for every one south door. Every step in latitude has twice as many rooms as the previous. I could draw a map of it like this:
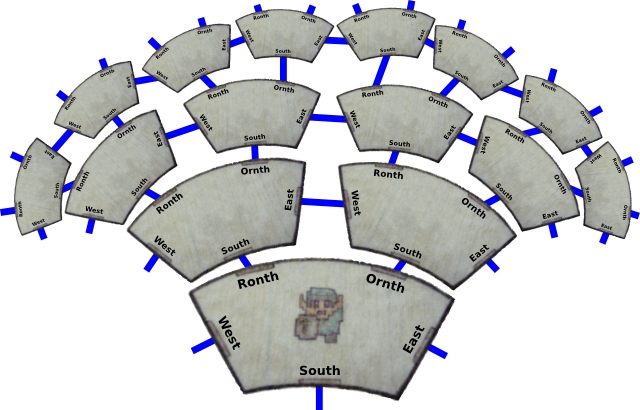
Map of a dungeon with two north doors for every south door; blue lines are hyperlinks connecting the rooms.
Since the two north doors lead in different directions, I’m calling them “ronth” and “ornth.” The rooms get very crowded at the top, so I decided to shrink them in my map. In the world of the video game, though, they’re all the same size.
Here’s a better way to represent them:

The dungeon modeled in cloth.
When these rooms are sewn together, they form a lumpy surface like a lettuce leaf. Our hero doesn’t know that: to him, it’s just a two-dimensional world. But there are many more places to explore than there are in the normal rectangular dungeon.
This is what it means for a space to be curved. We say that the cloth is curved because it cannot be laid flat due to the way that it is stitched— this is something more than merely folding a normal sheet of cloth. A curved cloth cannot be made uncurved without cutting or stretching. The two-dimensional space corresponding to that cloth is also curved. To make the correspondence explicit, imagine a computer screen pixel for every stitch in the fabric. The essence of curvature is the way that pixels— points in space— are connected to each other.
Despite his two-dimensionalness, the video game character knows that his world is curved. One experiment he can do is to measure the length of paths between two points:

Two paths from room A to room B. The lower one is a shorter path.
In an uncurved space, the shortest path between two rooms at the same latitude is a straight east-west line. To get from room A to room B, we might imagine that the shortest way would be to go east-east-east-east-east-east-east: 7 rooms. But in this space, south-south-east-ornth-ornth is shorter: 5 rooms. Even to our video game hero, this does not seem to be a straight path— first he’s going south, then he’s going ornth! But it is undeniably shorter: breadcrumbs prove it.
Experiments like this measure the degree of curvature. If the shortest path appears to be very curved, then the space-curvature must be very large. In an uncurved space (curvature equals zero), the shortest paths are perfectly straight lines. In a positively curved space, such as the surface of a globe, the shortest paths are great arcs: airplanes fly over Iceland on their way from Chicago to Switzerland. The video game space we’ve been considering here is negatively curved, and if we had three north doors for every south door, then it would be even more negatively curved.
Perhaps the most important example of a negatively curved space, apart from the crotch of my pants, is the world we live in. Close to the surface of the Earth, space-time is negatively curved. This curvature is very slight, but it is not zero.
To see the effect of this curvature in our everyday lives, we need to consider time as a dimension, like length, breadth, and height. Time intervals are distances, much like distances in space. Our perception of time is extremely foreshortened compared to our perception of space: one nanosecond of time is about as long as one foot. When we move, we trace out paths in space-time. Seen from the side, we are long, tapered creatures, only six feet high but three quintillion nanoseconds (95 years) long. And we lace around each other, threading through our lives like a mass of spaghetti.
Here is what a negatively curved space-time looks like:

Curved cloth representing height and time. (Note: this is only schematic, to convey the idea. The true shape is a little different.)
In this piece of cloth, the horizontal direction represents time and the vertical direction represents height. I drew the video game character incorrectly— in space-time, he would look like a snake, rather than having a back and a front that faces forward in time. I plead artistic license. In the time interval represented here, he leaps directly upward and falls back down. Apart from the initial leap, the course of his path through space-time is dictated solely by gravity.
That path is a parabolic arc. He rises, slows to a stop, and then falls back down at an ever-increasing rate. Though it is curved, this path is the shortest way from the initial position to the final one, much like the walk through the curved dungeon. If he had instead stayed on the ground, he would follow the rounded bottom edge through time, which is longer. The shortest paths through space-time are always falls.
According to General Relativity, that’s how gravity works. Skydivers feel weightless as they fall because they are: they are following the same kind of path through space-time as they would in deep space, far from the Earth. When we stand on the ground, we feel pushed into our feet. This is like the sideways push we feel in a car that is turning around a tight corner, for exactly the same reason: both are unnaturally long paths through space-time. Something must deflect our path from the natural one. When we stand on the ground, it is the solidity of the earth that prevents our feet from following the shortest path through space-time: straight down. When we turn a corner in a car, it is the seat-belt that prevents us from following the shortest path: straight ahead.
The curvature that causes a flying arc through the air to be a shorter space-time path than just staying on the ground is an extremely small one: our space-time is very nearly flat. On the second floor of a building, time intervals are only one part in a quadrillion longer than they are on the first floor. For a GPS satellite in orbit, an hour and one microsecond passes for every hour on the ground, and they need to be routinely synchronized to correct for this.
This tiny curvature is only noticeable to us because we have a foreshortened perception of time. It takes billions of nanoseconds— that is, a few seconds— to see the path of a tossed object deflect a few feet.
Though the Earth’s gravitational curvature is tiny, we are sensitive to the passage of time at exactly the right rate to be aware of it. It makes me wonder if this is a biological adaptation to living on Earth, much like the fact that we can only see the colors of light that can penetrate Earth’s atmosphere. Would creatures that evolve in low-gravity environments— asteroids— sense time much more slowly than us? Would creatures in high-gravity— the cooled husk of an ancient white dwarf star— seem to live at a maniacal pace?