
I like old science fiction. The stories from the first half of the twentieth century didn’t always get the science right, but they incorporated a lot of the latest ideas of their time. For example, When Worlds Collide, a 1934 novel about the Earth colliding with a roving exoplanet, had this description of the rocket that would save a remnant of humanity:
“Each of these tubes generates the rays that split atoms of beryllium into their protons and nuclei. The forces engendered in the process, which is like a molecular explosion, but vastly greater, together with the disrupted matter, is then discharged through this gun...”
Splitting atoms? Vast forces? They’re talking about nuclear energy ten years before the world knew about the atom bomb. But more surprisingly, the authors knew that beryllium might be a good atom to do it. Leó Szilárd’s secret patent two years later was based on the idea that beryllium or uranium might start a chain reaction— beryllium didn’t work, but uranium did.
Why did the authors, Balmer and Wylie, think that beryllium might be a good ingredient for a nuclear rocket? At the time, beryllium was used as a neutron source, and neutrons were known to increase the radioactivity of normal matter— but the neutron had only been discovered three years prior. Did they read scientific journals? Were these ideas “in the air,” known to a literate public?
Today’s science fiction usually doesn’t follow science this closely. Much of what I find in the modern stories is based on scientific ideas or discoveries that are at least fifty years old, like wormholes, antimatter, and parallel universes. If telepathy was ever considered scientific, then it was in the hyper-empirical environment of the 1920’s and 30’s, yet mind-readers are still ubiquitous in sci-fi. Did the science in science fiction congeal half a century ago?
In this article, I’m going to take a very recent theoretical idea and imagine what could happen if it were true. The borders of our knowledge are surrounded by dragons— anything that is not excluded by experimental data might exist, and can be taken seriously until proven otherwise. Thousands of theoretical papers postulate new laws of physics that could be discovered or refuted by the Large Hadron Collider (LHC) and other experiments. We group them into categories: Higgs and Higgs-like particles, the many variants of supersymmetry, extra dimensions (warped, universal, or large), and a potpourri called “exotica.” This one is definitely exotica.
The idea is that among the massive particles that are only found in the aftermath of violent collisions, there might be giant quarks, called quirks. This is a bit like saying that we know that lizards exist, and we know that giants exist (elephants, whales), so why not giant lizards? Tokyo is doomed! And in fact, giant lizards are possible— dinosaurs ruled the Earth. Quirks (with an “i”) are imagined to be ten or a hundred thousand times heavier than the lightest quarks. The top quark (with an “a”) is known to be 35 thousand times heavier than the lightest quarks, so it’s not at all impossible. The difference is that quirks would not decay immediately (as top quarks do) and would have their own quark-like force. It would be an isolated sector, similar to known particles, but unrelated to them.
Before talking about quirks, I need to explain what we know about quarks, a bit like a discourse on the humble ant before getting to the giant raging monster ants that are attacking the city. Quarks are attracted to each other by a very strong and sticky force. By “sticky,” I mean that the particles that cause the attraction between quarks are themselves attracted by this force. There is no analogue in our everyday world. The electric force that attracts hair to balloons is made of force-particles called photons, and photons don’t care about other photons— they just fly through each other. The quark-force particles, called gluons, veer toward other gluons.
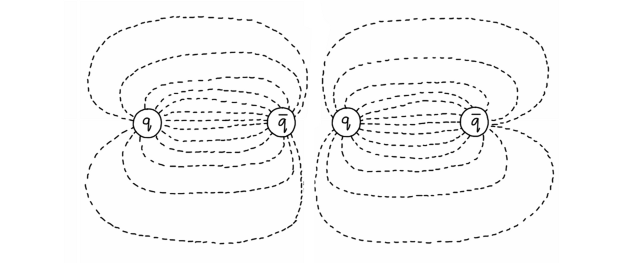
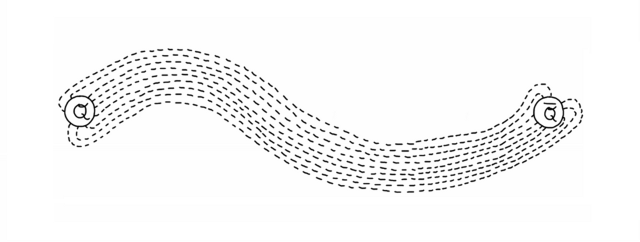
The lines of electric force between two oppositely charged particles (e.g. hair and balloon) look like the picture on the left. The lines of gluonic force between two quarks look like the picture on the right.
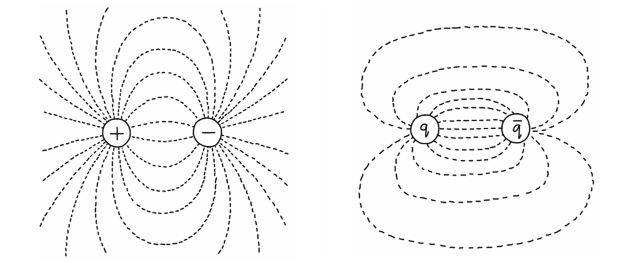
If we pull two charged particles away from each other, the lines of electric force spread out and the force gets weaker. If we pull two quarks away from each other, the lines don’t spread out because the gluons draw themselves into a tight bundle.
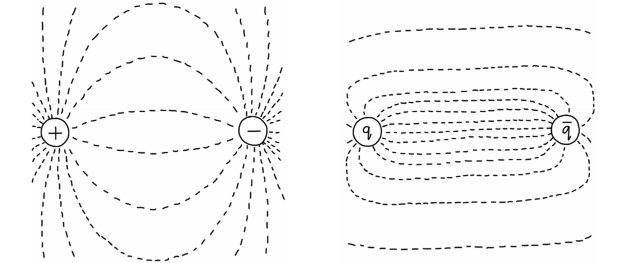
The force between the quarks doesn’t weaken with distance. It approaches a constant— approximately 14 tons. If we could separate the quarks by a distance large enough to see, they would have some amazing properties. But sadly, the tube breaks while the quarks are still within a millionth of a millionth of an inch. As the tube stretches, it accumulates enough energy to create two new quarks, which become the new endpoints of the tube.
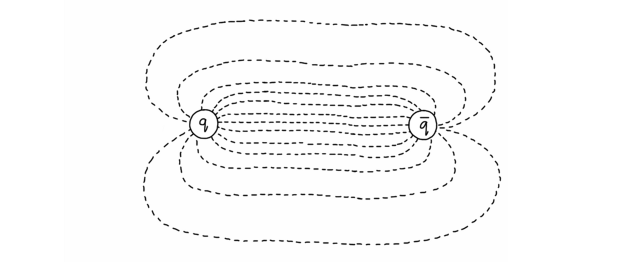
Here is how quirks differ: because quirks are so massive, it would take a lot more energy to create a new pair of them to break the tube. And since they’re hypothetical anyway, we can imagine that the quirk-force is weaker and puts less strain on the tube, too. (It’s a free parameter— it could have any value that hasn’t been ruled out.) There could be pairs of quirks flying out of the LHC right now, connected by subatomic rubber bands, spinning around each other like cannon balls tied by a chain. I say, “could be” because this particular theory has not been tested against LHC data, yet.
If the quirks, like quarks, are electrically charged, then we would see their trajectories in the detectors, looping around like a double-helix. Moreover, one of the quirks might even slow down and get lodged in a chunk of matter like the detector wall. If the other end of the tube is free, it would spiral around the fixed end until it loses enough energy to get stuck somewhere else. Then we would have a subatomic rubber band connecting two pieces of equipment.
One of the conditions of the quirk theory is that normal matter does not respond to the new quirk-force, only quirks do. Therefore, these tubes would pass right through normal matter like a ghost. (That’s not new: neutrinos do that, too, for the same reason.) Imagine what would happen if we got opposite ends of a lot of quirk strings lodged in two separate chunks of matter: the quirks are stuck to the normal matter because of their electric charge, and they are stuck to each other by the quirk-force. Thus, the normal matter would be bound together by this exotic force— imagine bridges in which we could walk through the supports or cranes whose cables can pass through buildings.
To get a crane that can lift a living-room couch from outdoors, we have assumed that the tubes can stretch many feet without breaking. Suppose that’s not true. If the parameters are such that they break when they’re a thousandth or a millionth of an inch long— much longer than subatomic scales but much shorter than human scales— they wouldn’t be useful for architecture. They would, however, be useful for materials science. Imagine a material that has been infused with quirks: a spiderweb of quirk pairs stretched across its atomic lattice. If we try to rip the material apart, not only would the normal atomic and molecular bonds resist the ripping, but so would the quirk pairs. If we pull hard enough, the quirk-tubes would break by forming new quirks— enriching the material even more. As we pull harder and harder, all of our effort would only create a denser and denser network of rubber bands, bracing the material more strongly than ever. Quirks would become the universal hardener— we could add them to any material to make it invincible.
Suppose that this sort of quirk is discovered with a mass of 1 TeV, which is the mass of a thousand protons. The energy needed to break a force-tube between two of them is twice the quirk mass, 2 TeV = 0.3 microjoules. If it breaks when it’s a thousandth of an inch long, then the average force they exert is work-divided-by-displacement = 13 millinewtons per pair. That’s not much force per pair, but the act of ripping them apart doubles the number of pairs. A thousand quirk pairs exert 13 newtons of force, which is 3 pounds, a million quirk pairs exert 1.4 tons, and 10 billion quirk pairs in a kilogram of meter-long material would be strong enough to build a space elevator. The quirk pairs double and redouble until we just can’t pull any harder.
Hardening a material in this way wouldn’t change its compressibility, since quirks don’t mind getting closer to each other. And it would only harden in the direction in which it is pulled, so we could make super-ropes or bullet-proof vests out of cotton. (Scratch that— the cotton would still deform when pushed by a bullet. It would follow the bullet with a finger-like extension through my chest. Yuck!) Another nice property is that we could release all of these quirks by melting the material: as the solid structure loosens, the quirk endpoints are released, allowing the rubber bands between them to pull together. When the quirk at one end meets the antiquirk at the other end, the two disappear in a puff of radiation. The material is now unquirked.
What could we do with a universal hardener? Perhaps we could get energy from uncontrolled nuclear fusion— hydrogen bombs. A volume of water 200 feet on each side would absorb all of the heat, but we would need an indestructible water balloon to contain the pressure wave. Suppose the indestructible water balloon has a hole in it pointing at a hydroelectric plant— that torrent of water would turn the turbines for a long time. Or suppose we lasso asteroids with a super-rope? Perhaps we could tie together two asteroids with specially chosen orbits so that they would be diverted toward Mars for some deep-crust drilling.
These are not predictions— we have no evidence that there’s any such thing as a quirk. It is one hypothetical scenario that I picked because I like thinking about its consequences. Scientists avoid speculating too far beyond established facts because the chain of “what if?” becomes too fragile: a single false assumption can bring down the whole house of cards. This is why it is so difficult to say what good will come of the discoveries made at frontiers like the LHC: those discoveries are so many steps away from their applications that any guesses are likely to be wrong. But science fiction can fill this gap. Even if the premise is as ridiculous as an exoplanet that just happens to collide with the Earth, it’s still fun to think about.