

I was stuck in traffic one day when a glorious double rainbow appeared over the highway. It had been a drizzly day; the whole sky was covered with clouds except for a little gap along the horizon, and it was just about sunset. As the sun slipped between the grey above and the ground below, the Chicago skyline was briefly golden with horizontal light, and two concentric rainbow rings encircled I-290 like a kind of tunnel.
Most of the rainbows I’d ever seen were faint wisps; this was an intense glow, as bright as a flask of electrified mercury. Fortunately, the cars weren’t moving, so I got a good, long look. Rainbow-like color separation happens a lot in physics classes, and I thought I understood what caused the second rainbow. I was wrong. I was thinking about first-order and second-order rainbows from diffraction gratings. If the rainbows in the sky were due to the same mechanism, the second rainbow would have to be twice as big as the first (it isn’t) and the colors would have to be in the same order (they aren’t). I stared at that second rainbow until the car behind me started beeping. Were my eyes deceiving me? Did the colors really go in the opposite order?
When I got home, I read all about rainbows and how they work. It’s fascinating: the story of its discovery spans twenty centuries.
The first part of the puzzle was solved by Aristotle (350 B.C.): why is the rainbow a bow? For reasons that were understood a thousand years later, water droplets in clouds reflect light at specific angles, primarily 42 degrees, and to a lesser extent, 51 degrees. As I drove east on the highway, the last rays of the sun were shining behind me. The rays that reflected off of the mist in front of me and into my eyes at a 42 degree angle collectively formed a circular ring. Water droplets inside the ring or outside the ring reflected rays that missed my eyes, so I didn’t see them. Half of this circular ring was underground, and the other half was the primary rainbow. Secondary rainbows come from droplets that reflect at 51 degrees.

If you try to reach a rainbow’s end, to get the pot of gold, perhaps, the rainbow would move. Different water droplets would reflect into your eyes so it would always seem to be the same distance, no matter where you go. In fact, this is probably what inspired the pot of gold story: it seems just like a fairy’s trick.
Aristotle understood the geometry, but his explanation of the colors and their intensities was wrong (Meteorologica, book III). He noticed that the most intense color in both the primary and secondary rainbows is red, but thought that this had something to do with the way that fires are red and the sun looks red when it is close to the horizon. Five centuries later, Alexander of Aphrodisias asked, “If so, then why isn’t the region between the two rainbows the brightest of all? Instead, it’s darker than both rainbows!” (paraphrase, see Lee and Fraser).

This prompted me to look at a lot of photographs of rainbows. It’s true: the band between the primary and secondary rainbow is often the darkest part of the sky. The main optical phenomenon is not the narrow strip of colors, but the bright circular disk within 42 degrees and the not-quite-as-bright annulus outside of 51 degrees. The colors are just a fringe that happen along the edges of these regions of light. It’s amazing how many paintings get this wrong.
Rainbows continued to be the bleeding edge of scientific research through the middle ages, with many Islamic scholars and Christian monks contributing to the problem. It often happens in science that the same discovery is made independently by two groups, simply because enough pieces of the solution are “in the air.” The idea of the Higgs boson, for instance, occured to three independent groups at the same time: it should be called a Higgs-Englert-Brout-Guralnik-Hagen-Kibble boson. The reason that water droplets reflect light within 42 degrees and outside of 51 degrees was solved simultaneously by Persian scholar Kamāl al-Dīn Fārisī and Dominican monk Theodoric of Freiberg in the first decade of the fourteenth century.
Fārisī and Theodoric both approached the problem with the combination of mathematical rigor and experimental honesty that defines modern science. They both filled spherical balls with water to simulate a raindrop, measured angles of light entering and leaving the ball, and used these measurements to arrive at a correct geometrical interpretation of how light bounces around inside. However, there were errors in the details that weren’t resolved until René Descartes solved the problem in 1637.
Descartes is my favorite philosopher-scientist. He developed two of the most important tools in mathematics: the use of letters as variables (e.g. y = x2 instead of “Consider a Quantitie, whose product of Itself with Itself is yet a seconde Quantitie, which will be determined forthwith...”) and analytic plotting. Plotting turns abstract relationships into pictures— profoundly useful in both math and science.
As in most fields, Descartes was unaware of prior results about rainbows and thought that he had invented it all himself. In fact, just to solve this problem he derived the law of refraction, which describes how light bends (refracts) when it passes from air to water or any other transparent medium. In the English-speaking world, we call this Snell’s law, since Willebrord Snellius discovered it 16 years earlier. In French, it’s called la loi de Descartes. It was originally discovered by Ibn Sahl of Baghdad in 984 A.D.
Here’s how rainbows work: when a ray of light enters a drop of water, it refracts at the air-water surface, part of it reflects inside the droplet, and then it refracts again on its way out. It may reflect once, twice, or many times inside the droplet, but it loses intensity with each reflection because part of the light passes through the back of the droplet, rather than reflecting. The inner disk of light (the primary rainbow) is due to one reflection and the outer annulus (the secondary rainbow) is due to two reflections. It’s hard to see rainbows from the third and fourth reflection because they come out of the back of the droplet, so you’d have to be looking toward the sun to see them.
The final angle of reflected light depends on where the incident light hits the droplet. A light ray that hits the middle of the drop does not refract at all— the water is simply a mirror. Light rays hitting the top of the droplet have the most complex behavior. The plot below shows the relationship between the location of impact and the final angle.
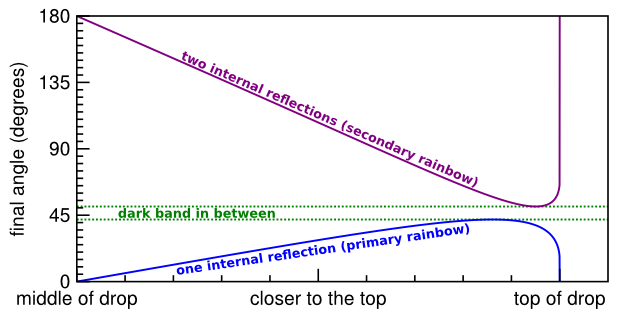
As you can see, the one-reflection case has a maximum of 42 degrees and the two-reflections case has a minimum of 51 degrees. They don’t overlap, so there is a band of no light between them. If the index of refraction of water had been 1.312, rather than 1.333, the primary and secondary rainbows would just barely touch each other, with no dark band.
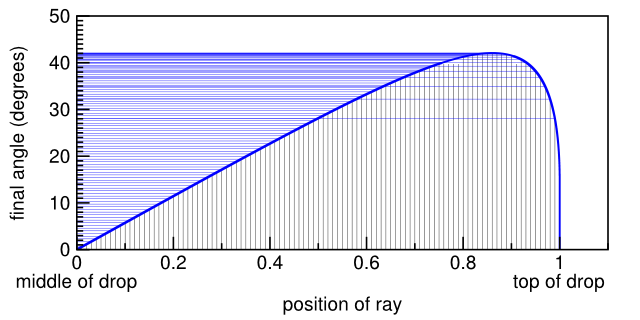
Rays of light are uniformly distributed along the droplet, but this leads to a non-uniform distribution of final angles. I’ve tried to show that in the plot below: uniform slices of the horizontal axis project non-uniformly on the vertical axis. Because the curve lingers at 42 degrees, there are more lines here than anywhere else.
Taking this a step further, the plot below shows the intensity distribution of final angles. Light rays pile up near 42 and 51 degrees, producing the most intensity at these two angles.
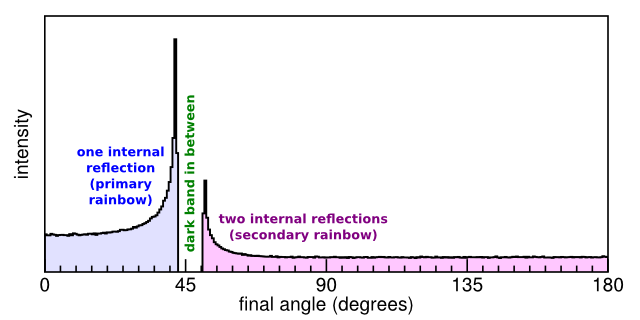
If we draw the intensity of each angle as a semicircle, it even begins to look like a double rainbow.

Except for color. Descartes’s theory completely accounted for the angles of the rainbows, the dark band, and even the shape of the intensity distribution, but didn’t have anything (correct) to say about color. That part of the problem was solved by Sir Isaac Newton 67 years later. Newton discovered that white light is not an indivisible entity but a mixture of all colors. In his experiments with prisms, he found that each color of light refracts at a slightly different angle.
As light enters and leaves a water droplet, red is refracted a little less than green, which is refracted a little less than blue. This pulls the light apart, especially at the extreme angles. It also explains the color reversal in the outer rainbow: the second mirror reflection switches the order of the colors.
The story doesn’t completely end there: Thomas Young explained supernumerary rainbows (mini-rainbows just below the primary) with his discovery that light is a wave (1804). In the 1820’s, Augustin-Jean Fresnel derived the equations that determine how much light reflects off of the back of the water droplet and how much passes through. There are even 20th century developments in theory and experiment.
However, the grand arc of the story begins with Aristotle and ends with Newton. Few problems in physics have engrossed so many scientists for so many centuries. It is a dramatic example of how science is cumulative: each discovery is only a part of a multigenerational quest. In fact, Newton’s famous quote about “standing on the shoulders of giants” was about this problem— the nature of white light and color separation in the rainbow. He wrote,
What Descartes did was a good step. You [Hooke] have added much several ways, & especially in taking ye colours of thin plates into philosophical consideration. If I have seen further it is by standing on ye shoulders of Giants.Newton to Hooke, February 1676; Corres I, 416
I knew a physics major who used this when he failed a test. “If I have not seen as far as others,” he said, “it is because giants were standing on my shoulders.”