
Imagine being invisible: what would that mean, physically? None of the skin, muscles, or bones in your body could absorb light in any way, including your eyes. Vision works because light is absorbed on the backs of your eyes, so to be invisible, you would also need to be blind.
Now imagine being intangible as well, imagine matter could pass through you as light does. You’d probably drop through the floor and orbit the center of the Earth like a yo-yo— that is, if you were insensitive to all forces except gravity. Take away gravity and there would be nothing left to tie you to this world. When light, matter, and gravity are not communicating with something, it might as well be in a separate universe. The extent of the physical world is defined by the interactions that connect our senses to phenomena: if something is truly undetectable, does it even make sense to say it exists?
Neutrinos inhabit a world that is almost, but not quite, disconnected from our own. They are insensitive to electromagnetism, the force that makes things visible and tangible, as well as the nuclear strong force that holds nuclei together in atoms. They ought to feel gravity but have so little mass that this has never been proven. We only know they exist because of their involvement in the weak nuclear force, which governs some but not all radioactive decays.
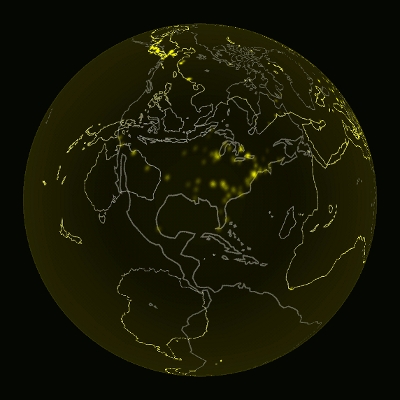
The picture above is the Earth— as seen in neutrinos. Neutrinos are emitted by uranium products in the Earth’s crust, but then pass pass through the Earth as though it were a soap bubble. The bright spots are new: they are nuclear power plants. To a weakly-interacting being who only sees neutrinos, nuclear reactors and atom smashers are the only evidence of life on Earth.
(Click here for a version that rotates. This graphic was created using data from the International Atomic Energy Agency’s Power Reactor Information System.)
Little Neutrinos
The idea of neutrinos started as a joke. “Dear Radioactive Ladies and Gentlemen,” Wolfgang Pauli wrote to a 1930 convention in Tübingen, “I have hit upon a desperate remedy to save the law of conservation of energy.” Certain radioactive decays seemed to be missing energy when all visible particles were accounted for. Pauli proposed that the missing energy was spirited away by an invisible particle, “but I dare not publish anything about this idea.” He then apologized for missing the meeting, as he was indispensable at a ball in Zürich.
Enrico Fermi took the idea and developed it into a complete theory of the weak interaction. He would have called this neutral particle a neutrone, but the word was already taken by a much more massive particle. Instead he called it “a little neutrino” with a pinch between the thumb and forefinger.
For twenty years, neutrinos were purely theoretical because they are so hard to detect. You have to build giant detectors and wait for one of the trillions of neutrinos passing through it each second to interact, causing a single atom to transmute (change from one kind of atom to another, like chlorine into argon). Neutrino detectors are usually room- or building-sized and are deep underground to protect them from the cosmic rays and other naturally occurring radiation that would transmute atoms much more easily.




Neutrinos are so inaccessible that their basic parameters are still not well known. They have mass, but not much and nobody knows how much. They come in at least three “flavors,” though there have been unconfirmed hints of a fourth. Like all other kinds of matter, they have an antimatter counterpart (antineutrinos), but unlike the others, there have been unconfirmed hints that antineutrinos have a different mass than neutrinos. Last year, an experiment seemed to show that some neutrinos travel faster than light. Though the result (now withdrawn) was met with skepticism, it got a lot more traction than it would have if it had not been about neutrinos. Physicists openly admit that they don’t much about this elusive particle.
Flavor Changes and Quantum Mechanics
I was still in college when it was first discovered that neutrinos spontaneously change from one flavor into another. All the professors in the physics department took Lincoln Wolfenstein out to lunch because this was (in part) his solution to the mystery of why we see fewer neutrinos from the sun than we expect. On their eight-minute journey to the Earth, about two-thirds of the neutrinos change flavors and seem to disappear in experiments that are sensitive to one flavor and not the others.
Neutrino flavors are defined by the reactions they participate in. Reactions involving electrons produce or consume electron-neutrinos, reactions with muons involve muon-neutrinos, and reactions with tau particle involve tau-neutrinos. For example, a nucleus can sometimes eat its innermost-orbiting electron, and when one of its protons uses it to transform into a neutron, it spits out an electron-neutrino, never a muon-neutrino or a tau-neutrino. Electrons, muons, and taus are very similar particles, differing only in mass. For unknown reasons, nature decided to have three electron-like particles and a neutrino for each of them.
Though flavor is a meaningful label for neutrinos traveling short distances, neutrinos lose their flavor-identity when they travel long distances. Electron-antineutrinos created in a nuclear reactor are still electron antineutrinos when measured in a detector less than a mile or so from the reactor. But most of the electron-neutrinos created in the sun become muon-neutrinos and tau-neutrinos on their way here: Earth-bound detectors find all three flavors, but a detector placed on the surface of the sun would see electron-neutrinos and little else (before it vaporized).
These neutrino transformations are a quantum mechanical effect, perhaps the largest quantum states ever seen. Quantum mechanics is usually only relevant for microscopic processes, like the energy of an electron orbiting an atom. A famous thought-experiment used to describe it is Schrödinger’s cat: a cat sleeps in an impervious box with a quantum measuring device attached to a vial of poison. If the device registers a certain value, it releases the poison and kills the cat. A quantum system can truly have multiple values for a parameter at the same time, such as an electron in two places at once or a light wave made of exactly five photons and also exactly ten photons. When measured, the quantum system randomly chooses to become one of the possibilities it had been considering. If nothing inside the box can be observed, the thinking went, the superimposed realities would carry through to the measuring device, the poison, and the cat. The cat would be both alive and dead, not one or the other.
This sort of thing doesn’t really happen with cats. Superimposed quantum states are delicate: though easy to produce on a microscopic scale, they quickly collapse (choose one possible value) when amplified to anything as large as a detector needle. If you were to try to build a real Schrödinger’s cat experiment, approximately half of your cats would be dead (unless you re-use cats), but none of them would be half-alive, half-dead. Quantum systems collapse whether anyone is looking at them or not, so making the box more impervious wouldn’t change anything but the epistemological question of how you can know if you don’t look. Though the collapse (or “decoherence”) of quantum systems is still not fully understood, the process seems to have something to do with the number of interactions. Isolated quantum systems maintain their concurrent realities, but systems pestered by frequent interactions from outside collapse to a single reality.
Few particles are as unharassed as neutrinos. Between a neutrino’s birth in the sun and its death in a detector, it interacts far less than an electron does when it jumps from your hand to a doorknob. For 93 million miles, the neutrino is in a womb of perfect isolation.
When a quantum system collapses, one variable describing it becomes single-valued while another becomes multivalued. (Sometimes people say “uncertain” instead of “multivalued,” but the latter is a better word.) The famous example is the duality between an electron’s position and its momentum (speed). Many simultaneous positions narrow to a single point in space as your position-measuring device interacts with it. But the same bath of interactions makes its momentum multivalued. Similarly, a wave-like light beam with a single-valued intensity can become a stream of a definite number of particles, depending on how you treat it, but not both. When a quantum system collapses, it doesn’t become non-quantum, it just chooses one way of being quantized over another.
Flavor and mass are the yin and yang of neutrinos. When a neutrino has a single flavor, it has three simultaneous masses, and when it has a single mass, it has three flavors. The production and decay of the neutrino are interactions that force a definite flavor: the sun makes electron-neutrinos and not muon-neutrinos or tau-neutrinos because it’s full of electrons, not muons or taus. (The sun is not hot enough to make muons and taus.) When a neutrino is destroyed by a reaction in an Earth-bound detector, the reaction can produce an electron, a muon, or a tau, but not more than one. Because the signals for these reactions look different, the quantum system collapses to only one at a time.
In transit, there are no demands on a neutrino’s flavor, but the mass becomes more definite. All particles acquire a more sharply defined mass as they fly away from an interaction, though the effect is most apparent for particles with ultrabrief lives. Particles living longer than a few yoctoseconds (a yoctosecond is a trillionth of a trillionth of a second) in a typical collider experiment have a single-valued mass within experimental resolution, while particles that die within a yoctosecond or less do not have time to choose a single mass. In the experiment, their mass appears as a smear that is wider than experimental resolution.
The Colors of Neutrino Mixing
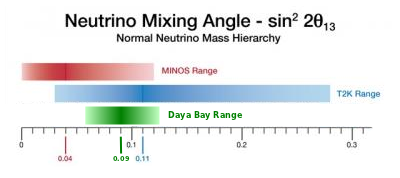
The duality between neutrino flavors and neutrino masses is what makes it possible for them to undergo a net change in flavor between the sun and the Earth. As the neutrino’s mass becomes single-valued, its flavor becomes triple-valued, and when it interacts, it randomly chooses one of those three flavors. That was a new discovery about a decade ago when I was in college. As of this month, we now know how much of each flavor is in each mass state. The Daya Bay experiment in China finally discovered the third and last mixing ratio (assuming there isn’t a fourth neutrino!). The T2K experiment in Japan and MINOS at Fermilab saw hints of this quantity last year, but not with enough certainty to claim a discovery.
The three neutrinos labeled by states of definite mass ν1, ν2, and ν3 have the following mixtures of electron-neutrinos (νe), muon-neutrinos (νμ), and tau-neutrinos (ντ):
| ν1 | is | 82% νe, | −44% νμ, | 37% ντ |
| ν2 | is | 55% νe, | 63% νμ, | −55% ντ |
| ν3 | is | 15% νe, | 64% νμ, | 75% ντ |
The exact numbers may change as measurements get more precise, but for the first time, none of them need to be left blank for lack of knowledge.
These numbers can be presented visually as a combination of colors. Suppose that νe, νμ, and ντ are red, green, and blue in a color palette. Each mass state would be a mixture of primary colors, like this:
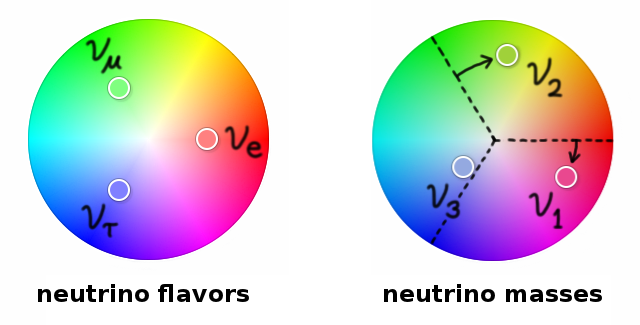
(Since some of the fractions are negative, I’ve chosen to represent zero as the grey halfway between black and white. Negative contributions are darker than half-grey. This paper was helpful.)
The mixtures are partly a rotation around the central point, but in the three dimensions of red, green, and blue. The new measurement from Daya Bay mostly accounts for the redness of ν3, which is slight. That’s why it was so hard to measure.
Neutrinos are not the only particles known to mix like this, but theirs is the most vigorous mixture. Three flavors of quarks, “down,” “strange,” and “beauty,” mix in the same sort of way. Though they have much shorter lives than neutrinos, these quarks spontaneously change flavor as they fly away from the collisions that created them. Their mixing looks like this:
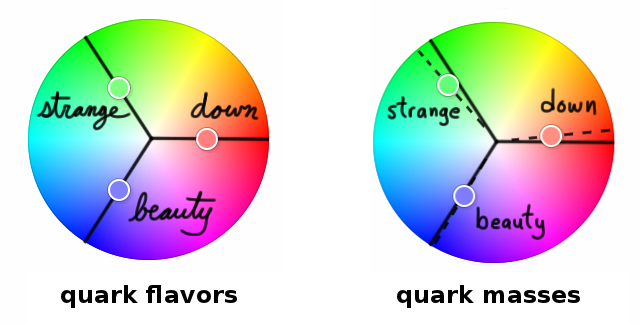
Notice that the mass states are barely any different from the flavor states, though there is a slight rotation. I’ve added guidelines to help you see it. There is so little difference that physicists don’t usually make a verbal distinction between beauty (by mass) and beauty (by flavor), as I’m doing with the block letters and cursive in the picture. Nobody knows why the quark mass and flavor states are so neatly aligned while the neutrino states are so wild. Nature may be trying to tell us something.
The Imaginary Part of the Mixture
In making these pictures, I’ve only had to sweep one fact under the rug. The proportions of flavor states in the mass states are complex numbers (see Wikipedia for more about complex numbers). Since I can’t mix complex fractions of red, green, and blue, I’ve assumed that the imaginary part of the mixing is zero. While this assumption is probably false, it’s still possible because the imaginary part hasn’t been measured yet.
However, this number I ignored might explain why we all exist. In the early universe, a slight difference arose somehow between the amount of matter and the amount of antimatter in the primordial soup. As the universe expanded and cooled, particles and antiparticles annihilated one another and were not replaced by new particle-antiparticle pairs from the ambient heat. If the matter and antimatter were exactly balanced, they would have completely annihilated, leaving nothing but an afterglow. Instead, the matter and antimatter almost exactly balanced, leaving mostly afterglow and a smidgen of matter. That’s us: all the stars and galaxies in the universe are the crumbs of a primeval feast.
Thirteen billion years later, we’re wondering how we survived. A slight difference between the laws governing matter and the laws governing antimatter could explain the imbalance, and the imaginary part of a flavor/mass mixing would provide such a difference. This motivated many careful measurements of quark mixing fractions, and the result of all that hard work is that we now know that quark mixing is too small to explain the primordial matter-antimatter asymmetry. Since the imaginary part of neutrino mixing is still unknown, one wonders if it was the neutrinos that tipped the scales.
Wouldn’t it be funny if our material world owes its existence to a particle that’s barely even here? Its imaginary fraction, no less?