
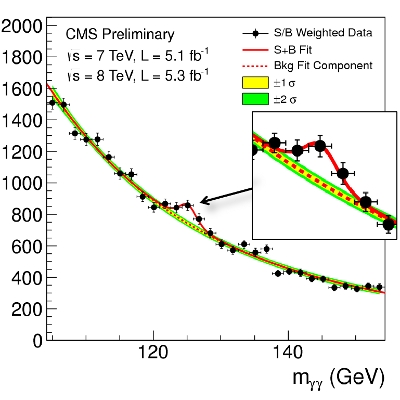
Two weeks ago, I learned something amazing and couldn’t tell anybody. I saw a plot like the one on the right: a new particle emerging from freshly unblinded data.
To avoid bias, scientists “blind” their data, hiding the most interesting part from themselves while they make sure that they understand all of the experiment’s calibrations and finalize the analysis procedure. When the physicists of the CMS Collaboration believed that the experiment was well-controlled, we all breathlessly looked at the Higgs data to see if last year’s hint might be reinforced. It was. In fact, it is now statistically robust enough to say that a new particle exists and it has some of the properties of the long-sought Higgs boson. This morning, the CMS and ATLAS Collaborations revealed their results to the world (and each other). The fact that such different experiments reached the same conclusion solidifies it: we’re probably looking at the first appearance of a particle hypothesized 48 years ago.
Why are physicists excited by one more particle? Statements like, “It gives mass to all the other particles,” are correct but beg the question, “Why should mass come from a new particle?” And what does that mean, anyway? Some physics topics are easy to motivate: a conversation about extra dimensions could begin with, “You know how there’s length, width, and height? Well, what if there are more than these three?” The Higgs Mechanism, however, solves a technical problem at the core of modern theories about matter and forces, and it requires a lot of background to even know that there’s a problem that needs to be solved. This boson’s “God Particle” epitaph hints that it plays a central role, but the name explains nothing and embarrasses physicists.
This article is intended to fill in what the newspapers leave out. Without assuming technical background, I’m going to try to explain why Peter Higgs and five other (uncredited) physicists independently invented the Higgs Mechanism, what that means, and why it’s so exciting to learn that they seem to have been right. The topic ties into so many different areas of physics that I have to fight the temptation to talk about all of them. I’ll try to get at the heart of the matter, if only by cutting away the rest of the body.
Strawberry Fields Forever
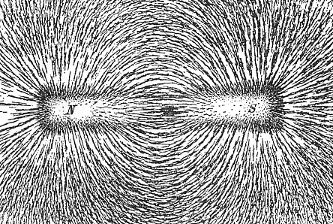
Magnetic field revealed by iron filings [source].
I can’t avoid starting with Quantum Field Theory, which is a particle physicist’s basic view of the world. Quantum Field Theory isn’t a single, specific theory but a framework for constructing theories that are consistent with Quantum Mechanics and Special Relativity. Specific theories are usually called models, like the Standard Model. The Standard Model revived interest in Quantum Field Theories in the 1970’s by being a surprisingly correct one.
Quantum Field Theory is a quantization of fields like the magnetic field. (I’ll get to quantization in a moment.) The field concept was invented to explain how magnets can affect metals from a distance. Instead of simply saying, “There is a force between the magnet and the metal,” we imagine that the magnet creates a disturbance in an invisible magnetic field, this disturbance propagates out to the metal, and then the field itself applies a force on the metal. All direct influences are local, and all long-distance influences are indirect, through mediating fields.

Haute tension!
This sounded too abstract to nineteenth century physicists, who preferred to think in terms of mechanics and physical objects. In its simplest form, a field is a purely mathematical construct: just numbers attached to each point in space. Magnets change the values of the numbers, and the values of the numbers apply forces. To give the field concept a mechanical basis, they supposed that all of space is filled with a very diffuse solid called aether, and the numerical values of the field are mechanical stresses in the aether. (The use of the word “tension” for electrical voltage is a relic of that idea.)
Albert Einstein took the opposite point of view. He assumed that the abstract fields were real and changed mechanics to conform to field theory— particularly the way that space and time are related in electro-magnetic fields. This imposition of field theory on mechanics is called Special Relativity, and it has some strange-sounding consequences for objects traveling close to the speed of light, the speed that disturbances propagate through a field. Nevertheless, experiments proved Special Relativity right and the aether theory wrong.
Nowadays, everything is a field. Not only is the attraction between magnet and metal supposed to be due to an enhancement of electromagnetic field values, but the atoms of the magnet and metal are themselves thought to be excitations of electron fields and quark fields. Early twentieth century discoveries in Quantum Mechanics undermined Newton’s idea of a “solid, massy, hard, impenetrable, movable particle,” and fields provide a workable alternative. In these experiments, electrons were seen to spread out and flow like the waves. Waves in an electromagnetic field appear to ball up and interact with matter in chunks. Neither is purely particle-like and neither is purely wave-like, so the exasperated conclusion in the 1920’s and 30’s was that both are both: matter and energy are waves and particles, particles and waves, and that is all ye need to know on Earth.
The state of physicists’ understanding has progressed since then— our current view is not quite as yin-yangy. The breakthrough (1940’s and 50’s) came from thinking about what the rules of Quantum Mechanics would do when applied to fields, not simply particle positions, as in Quantum Mechanics. Quantum Mechanics dissolves the position of a particle from a single point in space to a distribution of points. For instance, a particle that was thought to be 3 inches from a reference marker might turn out to be 25% at 2.9 inches, 50% at 3.0 inches, and 25% at 3.1 inches when you look closely enough. Quantum Field Theory dissolves each field value into a distribution of field values:
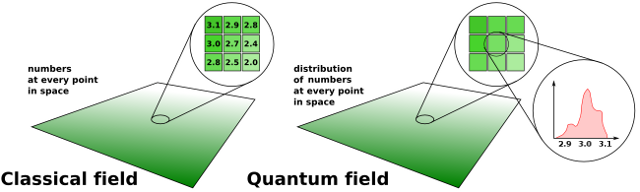
This is a more intricate picture than the original Quantum Mechanics because you not only have to imagine smeared out field values, such as 25% 2.9 Tesla, 50% 3.0 Tesla, and 25% 3.1 Tesla (Tesla is a unit of magnetic field), you also have to imagine a possibly different distribution at each point in space, across the universe.
Quantum distributions are not arbitrary, though. In the original Quantum Mechanics, Schrodinger’s equation restricted how electron clouds could fill a volume or react to a force. For technical reasons, this constraint usually reduces the set of allowed distributions to a finite or countable set of choices. That’s where the word “quantum” comes from: each distribution can be associated with a non-fractional number like 1, 2, or 3, which are called quanta. Here is what Quantum Mechanical electron distributions around an atom look like:
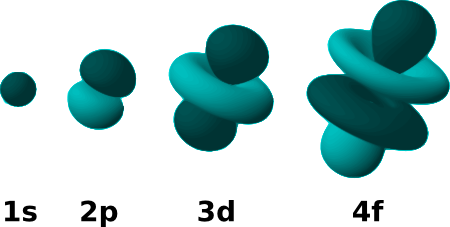
Some of the ways electrons distribute themselves in atoms, labeled by quantum number [source].
When a constraining equation is applied to quantum fields, they are similarly restricted to a countable set of choices. Whereas the pictures above are distributions of electron positions in space, the pictures below are distributions of field values at a single point in space:
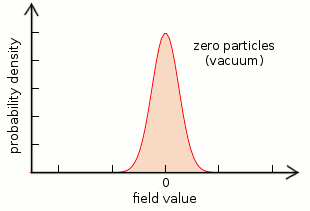
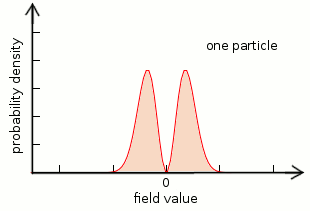
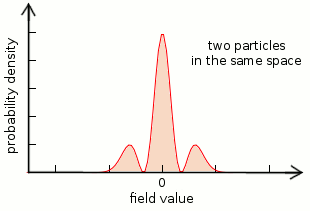
The first plot shows distribution zero, the next is distribution one, and the last is distribution two. (The series continues, but I’m only showing the first few.) According to the theory, distribution zero is a field without any particles, distribution one is a single particle, and distribution two is two particles at the same place at the same time. (Remember that these are field distributions for a single point in space.) The reason these can be called particles is because each configuration requires one more unit of energy than the last— to go from zero to one, you need to add one quantum of energy. That energy is the mass of the particle, and the transition between states is literally what it means to “create a new particle.” If one quantum of energy is released, the field returns to distribution zero, which is to say, the particle is destroyed.
In Quantum Field Theory, that’s all that a particle is: a field with enough energy to wiggle more than it usually does. Our experience of particles as chunks of something solid comes from the quantization, the fact that a “half-particle” is not allowed— there’s no distribution with half the energy. The Quantum Mechanical view of particle-wave hybrids doesn’t go far enough: there are only waves, but they are waves with quantized rest energy. There are no particles in particle physics.
This general discussion of particles and fields may seem out of place in an article about the Higgs boson, a particular particle of a particular field. But the Higgs Mechanism is a way of tinkering with fields to produce particle-like states in a completely new way. Without knowing where particles normally come from, it’s hard to appreciate how the Higgs is special. Before I get to the Higgs itself, I need one more topic: coupled fields.
The Web Wide World
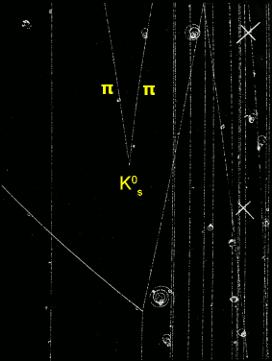
Particle physics is all about interactions among fields. An interaction is a transfer of energy from one field to another. For example, a one-particle excitation of the kaon field can transfer all of its energy to the pion field by creating a two-particle excitation in it. The kaon field then drops to its zero-particle state. In ordinary speech, we say that a kaon particle decays into two pion particles and we imagine a green ball (kaons are green) bursting apart into two blue balls (pions are blue), but we really mean that a quantized wave flows between the two fields.
Here’s a schematic of what that really looks like:
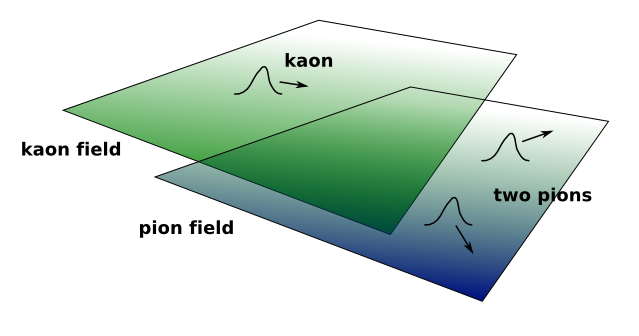
The hand-drawn bulge in the green field is the one-particle kaon excitation and the two bulges in the blue field are the pion excitations. Immediately after the kaon to two pion transition, both pions are in the same place at the same time, but they quickly separate because they fly away from their birthplace in opposite directions. For simplicity, I didn’t talk about energy of motion in the previous section, but a little kinetic energy is needed to balance the energy budget. A quantum of kaon has more mass-energy than two quanta of pion, so the motion of the pions makes up the difference.
Here’s what that looks like in real detectors, a bubble chamber from the middle of the last century (left) and the CMS experiment at the LHC (right). (The smearing-out of the particles is too small to see with these detectors, so the particle trajectories just look like streaks.)


Everything that particles do involves energy flowing from one field to another. As described above, particles decay by converting a one-particle state in one field into multiple-particle states in another field (or several other fields), but the exact reverse is also possible: particles brought together with enough speed can become a one-particle state in a more massive field. This is what particle colliders like the LHC do. We hope to discover new fields, such as the Higgs field, by exciting a one-particle state in it and observing what that decays into.
Ordinary forces, like the pull of a magnet, are also due to energy flowing between fields. Part of the motion of an electron in the magnet flows into the electromagnetic field, exciting a one-particle state (a photon), which drifts to another electron and gets absorbed as its motion. The net result is that the motion of both electrons changes, which is to say, they pulled or pushed each other with a force. Now I’m sliding off-topic because we only need to know about interactions in general, but I couldn’t resist telling you that all of the forces we feel when we yank a magnet off the refrigerator, push a door closed, or even taste food (chemical reactions are due to electromagnetic forces) are almost the same mechanism as the one that creates exotic particles out of motion and causes them to spontaneously decay.

A swing-set [source].
Why does energy flow between fields, anyway? The reason is close to the reason why swings on a swing-set can start each other rocking. If you get on a swing and ride it back and forth for a while, you may notice that the empty swings next to you wobble a little bit, too. The bar holding all swings together at the top of the swing-set is not perfectly rigid: your motion causes it to wiggle, and this motion is transferred to the other swings. The ones closest to you get most of the energy and rock the most, but the others farther away rock a little. The flow of energy from one field into another is an analogous effect.
Physicists call this a coupling: the swings are coupled to one another, with nearby swings coupled more strongly than the distant ones. We can just add couplings to a mathematical model of a swing-set to describe this behavior, though there’s a more fundamental reason for it— the metal it’s made out of is slightly elastic. Is there a more fundamental reason for the couplings between particle-fields? In some cases we know that there is: kaons and pions are made of more fundamental quark fields, and the kaon to two pion decay is an artifact of the strange quark to up quark and W boson decay. Nobody knows why the strange quark field is coupled to the up quark and W boson fields, but the strength of its coupling is accurately measured.
The universe is not only a profusion of different types of fields, but also a web of couplings between those fields. Each field fills all of space, and at each point in space it is connected to some other fields at the same point. The goal of particle physics is to discover all of the fields and measure all of the connections between them, laying out the web on paper as a mathematical model. Hopefully then we might see if there’s something beyond this paste-board mask.
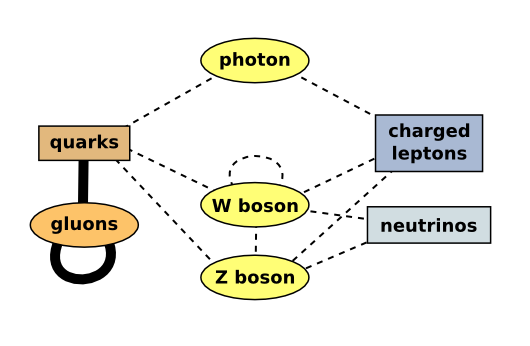
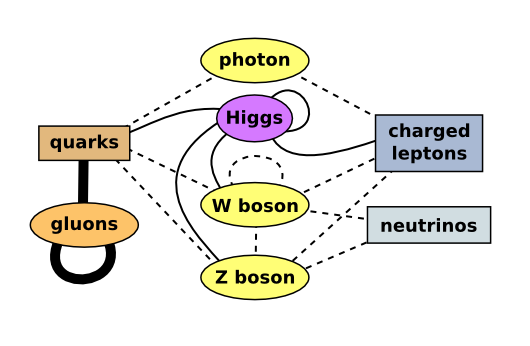
All known (as of yesterday) fundamental fields and their couplings. The photon, W boson, Z boson, and gluon are force fields, while the quarks, charged leptons (e.g. electrons), and neutrinos are matter fields.
The Problem that a Higgs Boson Would Solve
Quantum Field Theory provides a nice picture of the universe. Very little was added by hand— we didn’t have to assume that the universe is full of particles because particles are a natural consequence of quantum fields, which we were already using to explain forces. All of the particle decays, annihilations, and simple forces are described by a single mechanism: couplings between fields. But physicists are greedy— we can get a little more for nothing.
If the equation constraining the matter fields has certain symmetries, then the forces are not arbitrary; they’re required to exist. That is, the forces would be a natural consequence of the symmetries. Though we can’t explain why our universe is so symmetric, we can say that it must have electromagnetic, radioactive, and nuclear forces because of the symmetry. (Gravity derives from a space-time symmetry in General Relativity— what I’m discussing here extends that concept to all of the other forces using non-space-time symmetries.) For the sake of argument, I’ll use mirror symmetry as a stand-in for the symmetry that “generates” the forces, though the true geometry of it is much more intricate.
Note how the field distributions corresponding to any number of particles is mirror symmetric around zero:



That is, if you fold the distribution along the zero-line, the left side matches the right side. While it may be easy to enforce a symmetry like that at a single point in space (just don’t make explicit reference to the sign of the field values), it’s harder to enforce it at all points in space simultaneously. Particles mix field distributions as they move from point to point and would ruin the symmetry unless a new term is added to the equation. That term is a force that couples to the motion of the particle. By assuming the symmetry, we are required to add the force— we’re closer to knowing why the force exists.

The famous T-shirt, replacing an explicit force law with the symmetry that generates it [source].
All of that works for one force, electromagnetism. In the 1940’s and 50’s, physicists like Sin-Itiro Tomonaga, Julian Schwinger, and Richard Feynman assumed the existence of an electron field with a simple symmetry (the one on the T-shirt) and all electric and magnetic forces fell out of it, fully consistent with Quantum Mechanics and Special Relativity. Physicists expected the same to work for radioactivity, though with a more complex symmetry because there are two fields responsible for this force: the W boson and the Z boson.
The problem was that W and Z bosons are massive (discovered in 1983-4, they have masses of 80.4 and 91.2 GeV, respectively). In Quantum Field Theory, mass is a coupling of a field with itself: the energy flows from itself to itself, without going anywhere. Another way of looking at it is to say that the field has a potential energy curve that looks like this:
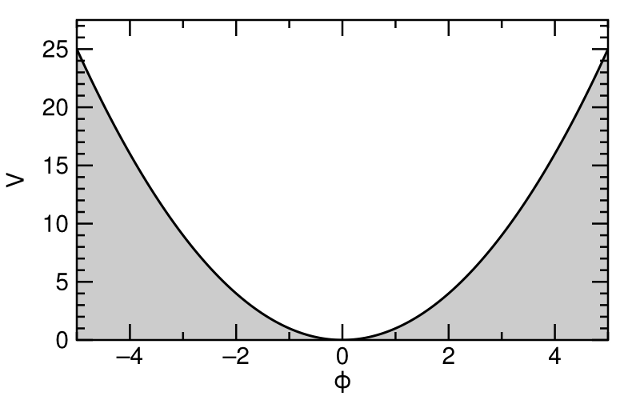
Potential energy (V) versus field value (ϕ) for a massive field.
Potential energy is an energy cost: this plot says that field values (ϕ) near zero don’t require much energy, but field values far from zero do. It is similar to the potential energy of a swing on a swing-set. Not much energy is needed at the bottom of the swing’s arc, but it takes a lot of pumping to get up high, on either side (usually back and forth). This is why the zero-particle distribution consists mostly of values near ϕ = 0 and the one and two-particle distributions have more values far from zero. It costs energy to make a one or two-particle state.
The original formulation of Quantum Electrodynamics had a term like this to describe the electron’s mass. There was no need to add a similar term for the photon because photons are known to be massless. In fact, if you tried to add it, the equation would no longer be symmetric, which undermines the whole project. The point was that the symmetry generates a force automatically, but if you try to add a mass to that force particle, you lose the symmetry and therefore lose the force.
While this was a lovely explanation of Quantum Electrodynamics, it was unworkable for the radioactive force with its massive W and Z bosons. That’s the problem.
How a Higgs Boson Solves It
The solution came together in 1964 in a series of papers by Robert Brout, François Englert, Gerald Guralnik, C. Richard Hagen, Tom Kibble, and Peter Higgs. Somehow, it came to be known as the Higgs Mechanism. Instead of adding a mass term for each known-to-be-massive particle by hand, they assumed that fundamentally, no particles have any mass except for a new, undiscovered Higgs boson. Moreover, the Higgs field has a very strange-looking potential:
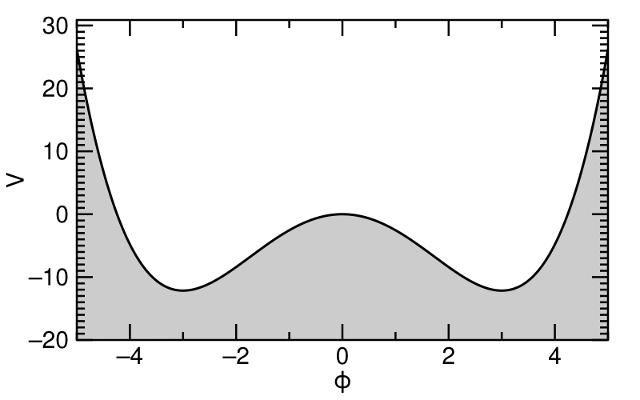
Potential energy (V) versus field value (ϕ) for the Higgs field.
This potential doesn’t have a minimum at zero— it has multiple minima that are far from zero (just above 3 and below −3 in my plot). Particle-like excitations of the Higgs field are completely unlike those of normal fields, too. The zero-particle distribution is not clustered around ϕ = 0, but ϕ = 3 or ϕ = −3. Sometime in the early moments of the universe, the Higgs field slid into one lobe, like a car tire that gets stuck in one rut rather than another. The Higgs field has one-particle excitations, two-particle excitations, etc., but these are all centered on the minimum that it fell into, like the car trying (unsuccessfully) to drive out of the rut.
The Higgs field also must couple to the W and Z fields. These fields don’t have any mass on their own, but their coupling with the Higgs makes them look like they do. A coupling from a W boson to a Higgs field back to the W boson looks just like a coupling from a W boson back to itself, as long as the value of the Higgs field is far from zero. The fact that the Higgs is stuck in a rut, far from zero, guarantees this. This mathematical trickery saves the symmetry that generates forces and also saves the phenomena, the empirical observation that W and Z bosons look like they have masses.
All known fundamental fields, including the Higgs field.
Thus the W mass term is “made out of” part of the Higgs field. If there were a patch of space with , the W boson would be massless there.
A little more detail, using undergraduate calculus.
In fact, it’s such a neat mechanism for giving masses to the W and Z bosons that it might give masses to all other particles as well (except neutrinos— their masses are very small and are probably from a different mechanism). Let’s stop here and take stock of what this whole picture gives us.
It’s a beautiful theory. The only problem with it— for the last half century— was that it wasn’t proven.
What we Know Today (as Opposed to Yesterday)
This Higgs Mechanism is such a crucial piece of the Standard Model that experiments have sought evidence of it for decades. According to the theory, we’re bathing in Higgs field— almost every point in the universe has a Higgs field sitting in a ϕ = 3 or −3 lobe of its potential. In real units (“3” is a made-up unit in my plot), this is 246 GeV: about three times the W boson mass. But if everywhere is the same, you can’t experimentally prove that the Higgs field is there at all.
To prove that it exists, we must excite the Higgs field into at least its one-particle state by feeding it energy. We collide protons at very high kinetic energies with the hope that some of this energy will leak into the Higgs field, briefly create a Higgs particle, which then decays into any of the particles that couple to the Higgs. The decay products would show up as a blip of extra events, all at the same mass.
Here are the blips. The CMS and ATLAS experiments took zillions of pictures of proton collision debris (I don’t know the order of magnitude, but it’s huge). They applied sophisticated machine learning algorithms to identify Higgs-like events and made histograms of the rest mass of pairs of particles (photons and Z bosons in the examples below). Most of the events in each plot are not Higgs-related, but there’s a consistent peak at 125 GeV that can’t be explained by other processes. It looks exactly like a new particle.
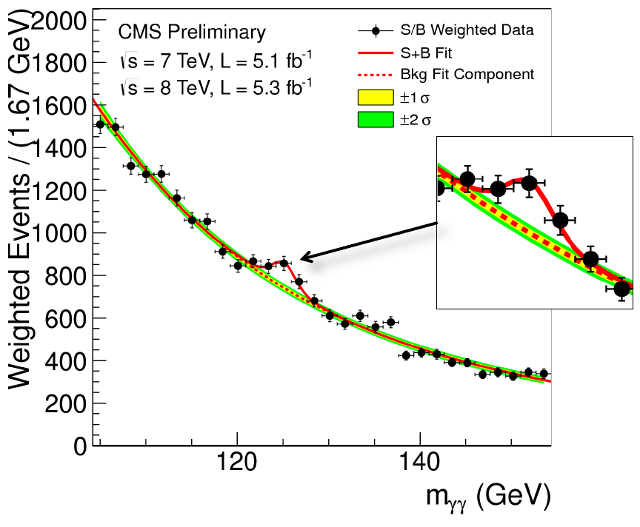
The two photon spectrum as seen in CMS. The few events clustered around 125 GeV are the new boson decaying into two photons; the rest are due to unrelated particles decaying to two photons.
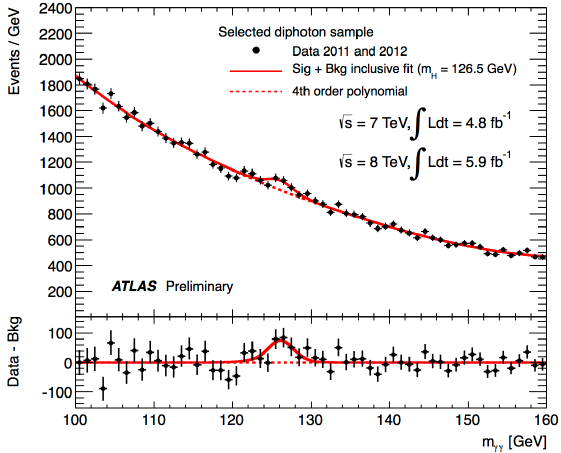
The two photon spectrum as seen in ATLAS. Same interpretation.
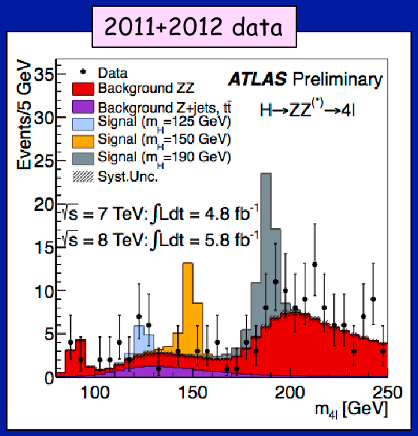
The two Z boson spectrum as seen in ATLAS. The events clustered around 125 GeV (light blue) are the new boson decaying into two Z bosons; the rest are unrelated. (The red peak at 90 GeV is “single Z with final-state radiation” and the larger red hump at 200 GeV and above are true double-Z events, but not Higgs related. The yellow and grey peaks are what a Higgs boson would look like if it had a mass greater than 125 GeV.)
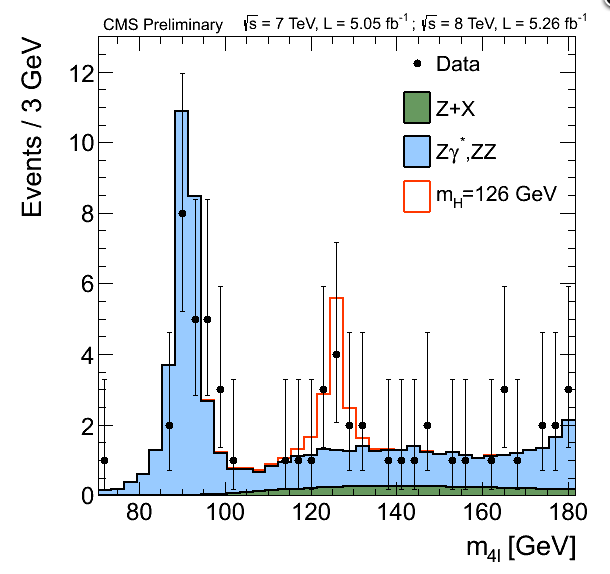
The two Z boson spectrum as seen in CMS. ATLAS’s red distribution is light blue in CMS’s plot, and ATLAS’s light blue distribution is red in CMS’s plot.
These signals are just barely significant, but they’ve crossed the “five sigma” discovery level (per experiment), which is more than a one in a million chance that the signal is a random fluctuation. We know that the new particle decays into pairs of photons and pairs of Z bosons, which means that it must be a boson. We don’t know that it’s a Higgs boson because a Higgs boson must have a particular set of couplings to known fields, and we’ve only seen two couplings: new boson to photon and new boson to Z. These two are consistent with being a Higgs boson, but there’s still enough wiggle room for this particle to have nothing to do with giving masses to particles. If it’s not a Higgs, then we have no idea what it is.
Far from being the end of a search, this discovery may mark the beginning of direct studies of the Higgs boson. This lovely theory of forces generated by symmetries and masses generated by a Higgs field may still be incomplete— the only way to know is to test it. If the rest of this year’s data support our suspicion that “the 125 GeV boson” is actually the Higgs boson (or “a” Higgs boson, from a non-standard model), then we may finally have the tools to find out.